 Optimization: Full Optimization: Search 0
Optimization: Full Optimization: Search 0
В этом разделе:
— определение стадий оптимизации, которые проходит запрос;
— структура для поиска альтенатив memo;
— оператор Apply lookup в nested loops join;
— оценки и вычисления селективности запроса с несколькими предикатами;
— стоимость операторов;
— Rebind, Rewind, RowGoal;
— просмотр начального и конечного memo;
— выходное дерево физических операторов;
Эта фаза, также известна как Transaction Processing, она может быть пропущена, если таблиц в оптимизируемом запросе менее трех. Но прежде всего, как определить, на какой стадии была прекращена оптимизация запроса. В случае с тривиальным планом, это отображается в плане, в корневом операторе в свойстве Optimization Level, значением TRIVIAL. Как можно определить стадию, если в плане отображается просто уровень FULL. Есть несколько способов.
Первый, это прибегнуть к запросу еще одной недокументированной DMV, sys.dm_exec_query_optimizer_info.
В этом крайне интересном представлении содержится много различных счетчиков, в частности можно посмотреть информацию о количестве оптимизаций, оптимизаций с хинтами, количестве истекших таймаутов, превышений памяти, подзапросов, нераскрытых подзапросов и т.д. Здесь мы используем ограниченное число этих счетчиков, только с целью определить, какие стадии оптимизации прошел запрос.
Для этого, используем ту же тактику сравнения снэпшотов до и после выполнения запросов и вычисления разницы, как и в случае с просмотром правил трансформации.
select * into BeforeQ from sys.dm_exec_query_optimizer_info where [counter] in ('trivial plan','search 0','search 1','search 2');
go
select * into AfterQ from sys.dm_exec_query_optimizer_info where [counter] in ('trivial plan','search 0','search 1','search 2');
go
drop table BeforeQ,AfterQ;
go
select * into BeforeQ from sys.dm_exec_query_optimizer_info where [counter] in ('trivial plan','search 0','search 1','search 2');
go
select
*
from
t1
join t2 on t1.a = t2.b
join t3 on t2.b = t3.c
where
t1.b = 1
option(recompile)
go
select * into AfterQ from sys.dm_exec_query_optimizer_info where [counter] in ('trivial plan','search 0','search 1','search 2')
go
select
a.[counter],
occured = (a.occurrence - b.occurrence)
from
BeforeQ b
join AfterQ a on b.[counter] = a.[counter]
where
a.occurrence <> b.occurrence
;
drop table BeforeQ,AfterQ;
go
Результат:
|
Давайте вернемся к предыдущим запросам, выполним их и посмотрим, что нам вернет статистика. Я не буду приводить здесь этот код, т.к. работает просто метод copy/paste, вместо исследуемого запроса, просто подставляйте приведенные ниже, не забывая про опцию recompile.
select b from t1 where b >= 1 option(recompile)
|
Как мы видим, этот запрос удовлетворяет тривиальному плану.
Теперь, если вы замените в фильтрах статистики стадии на информацию по подзапросам (не забудьте поменять во всех частях запроса, причем так, чтобы в части для кэша планов, запрос совпадал с частью делающей снэпшот, вплоть до символа, так что используйте copy/paste):
select * into BeforeQ from sys.dm_exec_query_optimizer_info where [counter] in ('contains subquery', 'unnest failed')
select * into AfterQ from sys.dm_exec_query_optimizer_info where [counter] in ('contains subquery', 'unnest failed')
То увидите что подзапрос:
select t1.b, t1.c, d = (select min(c) from t3 where t1.c = t3.c) from t1 option (recompile)
Вернул:
|
Т.е. оптимизатор увидел, что в нем есть подзапрос, и раскрыл его (как мы помним из предыдущей части).
А запрос:
select t1.b, t1.c, d = (select top(1) min(c) from t3 where t1.c = t3.c) from t1 option (recompile)
Вернул:
|
Т.е. оптимизатор также увидел подзапрос, но не смог его раскрыть для предложения top (unnest failed), о чем мы тоже говорили.
Теперь, верните фильтры для просмотра стадий оптимизации, закомментируйте в изначальном запросе одно соединение и выполните:
select * from t1 join t2 on t1.a = t2.b --join t3 on t2.b = t3.c where t1.b = 1 option(recompile)
результат:
|
Т.е. фаза search0, о которой мы сейчас говорим, была пропущена, и состоялся переход сразу к фазе 1. Тут срабатывает одно из условий удовлетворения запроса фазе search0, эта фаза применяется для запросов с как минимум тремя таблицами, если их меньше – обработка переходит сразу на фазу search1.
Еще один способ, посмотреть на стадии оптимизации — это задействовать недокументированный флаг 8675. Он выводит некоторую служебную информацию по стадиям оптимизации.
Включим Include Actual Execution Plan и выполним исследуемые ранее запросы:
set nocount on
go
print('--------------------
trivial plan:')
select b from t1 where t1.b = 1
option(recompile, querytraceon 3604, querytraceon 8675)
go
print('--------------------
search 0:')
select * from
t1
join t2 on t1.a = t2.b
join t3 on t2.b = t3.c
where
t1.b = 1
option(recompile, querytraceon 3604, querytraceon 8675)
go
print('--------------------
search 1:')
select * from
t1
join t2 on t1.a = t2.b
--join t3 on t2.b = t3.c
where
t1.b = 1
option(recompile, querytraceon 3604, querytraceon 8675)
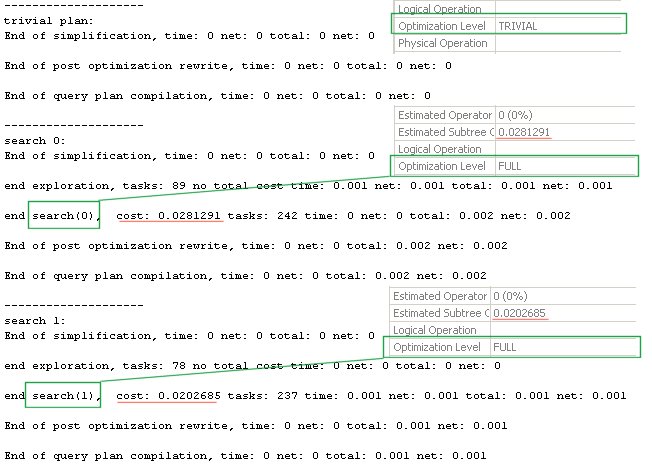
Переключимся на вкладку Messages — результат:
Обратите внимание, что данный флаг не вывел что уровень оптимизации trivial в первом запросе, однако мы и так можем это легко узнать, поглядев на свойства в плане. Зато он вывел информацию по стадиям search 0 и search 1 соответственно, кроме того некоторую другую информацию. В частности, например, мы видим, что cost (стоимость) на последней фазе, совпадает с той, что указана в плане. Значение tasks – содержит информацию об операциях оптимизации, которые могут включать в себя исследовательские задачи, выводу свойств и применению правил, и т.д.
Также обратите внимание, что каждой фазе (search0,search1) предшествует фаза exploration. На этой фазе могут применяться исследовательские правила преобразования, например, JoinCommute — для перестановки соединений, и строится изначальная структура для поиска альтернатив при построении плана.
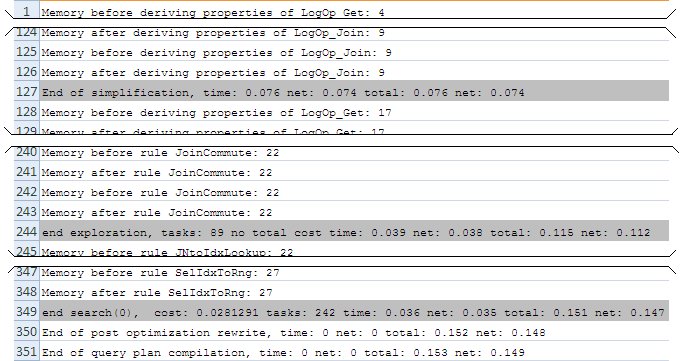
Если комбинировать этот флаг трассировки с флагом из предыдущей части, по выводу свойств и применению правил, то можно увидеть вот такую картину:
Прежде чем идти дальше, удалим созданный по колонке t1.b индекс.
drop index ix_b on t1;
И выполним обновление статистики во всех таблицах, для более точных оценок:
update statistics t1 with fullscan; update statistics t2 with fullscan; update statistics t3 with fullscan;
Memo
Для поиска альтернатив и выбора наиболее дешевых вариантов, оптимизатор использует структуру Memo. Она начинает использоваться на стадии полной оптимизации (т.е. со стадии search 0, о которой мы сейчас говорим), для тривиального плана она не создается. На каждой стадии оптимизации создается новая структура. Я думаю, более понятно, что это такое и как работает, будет, если объяснить это на примере. Возьмем наш запрос для стадии поиска 0.
Прежде всего, выполним его, с флагом трассировки, который покажет нам логическое дерево операторов.
select * from t1 join t2 on t1.a = t2.b join t3 on t2.b = t3.c where t1.b = 1 option(recompile, querytraceon 3604, querytraceon 8606) go
Возьмем последнюю, из показанных, стадию его преобразования: Tree After Project Normalization.
Вот как оно выглядит:
LogOp_NAryJoin
LogOp_Select
LogOp_Get TBL: t1 t1 TableID=226099846 TableReferenceID=0 IsRow: COL: IsBaseRow1001
ScaOp_Comp x_cmpEq
ScaOp_Identifier QCOL: [opt].[dbo].[t1].b
ScaOp_Const TI(int,ML=4) XVAR(int,Not Owned,Value=1)
LogOp_Get TBL: t3 t3 TableID=370100359 TableReferenceID=0 IsRow: COL: IsBaseRow1007
LogOp_Get TBL: t2 t2 TableID=306100131 TableReferenceID=0 IsRow: COL: IsBaseRow1004
ScaOp_Logical x_lopAnd
ScaOp_Comp x_cmpEq
ScaOp_Identifier QCOL: [opt].[dbo].[t2].b
ScaOp_Identifier QCOL: [opt].[dbo].[t3].c
ScaOp_Comp x_cmpEq
ScaOp_Identifier QCOL: [opt].[dbo].[t1].a
ScaOp_Identifier QCOL: [opt].[dbo].[t3].c
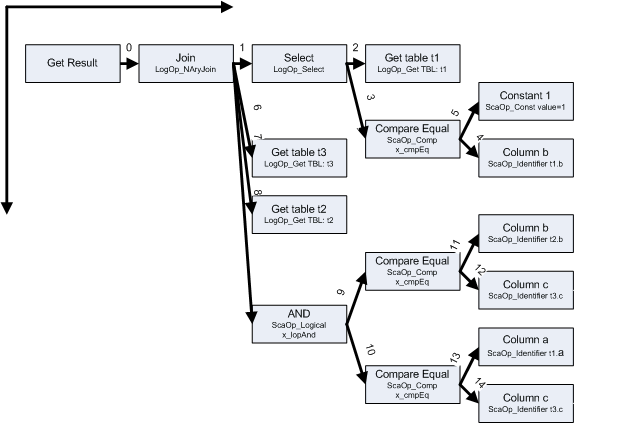
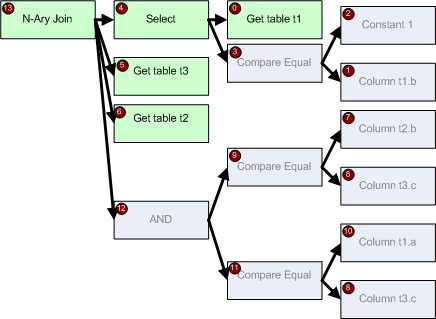
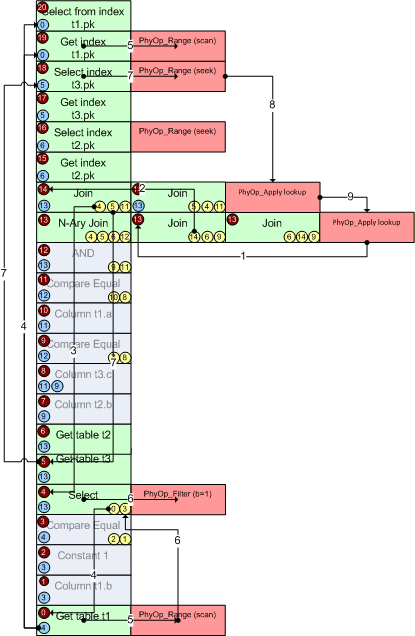
Чтобы было понятнее, я изобразил его графически:
Читаем логику, слева направо и сверху вниз.
0 — для получения результата
1-соединение
2 — получить таблицу t1
3 – проверить равенство
4 – колонки b
5 – константы 1
6 — получить данные из таблицы t3
7 – получить данные из таблицы t2
8 – выполнить логический and выражений
9 – проверить равенство
10 – колонки t2.b
11 – колонки t3.c
12 — проверить равенство
13 – колонки t1.a
14 – колонки t3.c
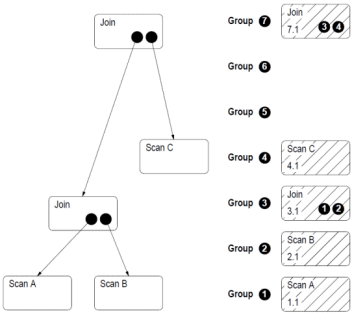
Теперь, поместим наше дерево в memo следующим образом. Каждый логический оператор, помещается некую группу, группу эквивалентности и по мере применения правил преобразования в этой группе могут возникать новые логические или физические операторы.
Также могут возникать и новые группы эквивалентности. Например, t1 join t2 = группа 1. Группа 1 join t3 = Группа2. Но можно сделать и по-другому t1 join t3 = группа 4. Группа 4 join t2 = Группа 5. Т.е. были созданы две новые группы 4 и 5.
В группах может происходить взаимодействие, как с логическими операторами, так и с другими группами. Как, например, в группах 2 и 5, где взаимодействуют непосредственно операторы получения данных из таблиц и результаты других групп.
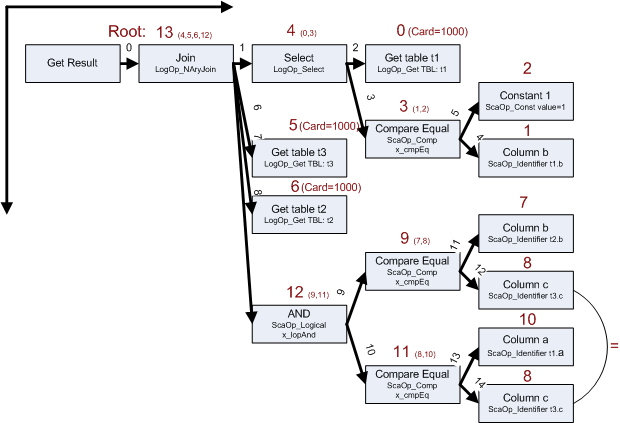
Может быть сейчас непонятно, но на картинке станет понятнее. Ниже, даны пояснения.
Начнем последовательно с первого оператора Get table, кроме того, для этих операторов, мы можем сразу из метаданных записать информацию о количестве строк таблицы, для которой выполняется этот оператор, т.е. взять Cardinality (Card) таблицы.
Итак:
В группу 0 поместим логический оператор получения таблицы 1 (кол-во строк 1000);
В группу 1 поместим скалярный оператор получения колонки t1.b;
В группу 2 поместим скалярный оператор получения константы 1;
В группу 3 поместим результат скалярного оператора Compare Equal над двумя предыдущими результатами (группа 1 и группа 2 — обозначены на рисунке в скобках, мелким шрифтом);
В группу 4 поместим логический оператор выбора результата групп 0 и 3;
В группу 5 поместим логический оператор таблицы 3 (кол-во строк 1000);
В группу 6 поместим логический оператор таблицы 2 (кол-во строк 1000);
В группу 7 поместим скалярный оператор получения колонки t2.b;
В группу 8 поместим скалярный оператор получения колонки t3.c;
В группу 9 поместим результат скалярного оператора Compare Equal над двумя предыдущими результатами (7 и 8);
В группу 10 поместим скалярный оператор получения колонки t1.a;
В группу 11 поместим результат скалярного оператора Compare Equal над двумя предыдущими результатами (10 и 8) – ведь вспомним, что мы уже получили колонку t3.c в группе 8;
В группу 12 поместим скалярный оператор AND двух предыдущих результатов, групп 9 и 11;
В группу 13 поместим логический оператор соединения результатов всех предыдущих групп 4,5,6,12.
Теперь, поместим результат в таблицу:
Итак, мы закончили. Насколько это соответствует правде?
Проверим! Есть очередной недокументированный флаг трассировки, чтобы посмотреть изначальную структуру Memo. Выполним:
select * from t1 join t2 on t1.a = t2.b join t3 on t2.b = t3.c where t1.b = 1 option(recompile ,querytraceon 3604 ,querytraceon 8608 --изначальное memo )
Результат:
--- Initial Memo Structure --- Root Group 13: Card=10 (Max=10000, Min=0) 0 LogOp_NAryJoin 4 5 6 12 Group 12: 0 ScaOp_Logical 9 11 Group 11: 0 ScaOp_Comp 10 8 Group 10: 0 ScaOp_Identifier Group 9: 0 ScaOp_Comp 7 8 Group 8: 0 ScaOp_Identifier Group 7: 0 ScaOp_Identifier Group 6: Card=1000 (Max=10000, Min=0) 0 LogOp_Get Group 5: Card=1000 (Max=10000, Min=0) 0 LogOp_Get Group 4: Card=10 (Max=10000, Min=0) 0 LogOp_Select 0 3 Group 3: 0 ScaOp_Comp 1 2 Group 2: 0 ScaOp_Const Group 1: 0 ScaOp_Identifier Group 0: Card=1000 (Max=10000, Min=0) 0 LogOp_Get ------------------------------ (10 row(s) affected)
Если вы удалите излишние переносы строк и приведете к табличному формату, то вот что вы увидите:
Практически полное соответствие тому, что мы проделали.
Далее, начинается процесс поиска альтернатив и применения правил преобразования. Собственно, если построение первоначальной структуры memo, при нашем простом запросе, еще было более или менее простым и предсказуемым, то предугадать результат дальнейших действий оптимизатора трудно. Ответ на этот вопрос могут дать разве что люди из MS, у которых есть обширные знания механизмов выбора правил, алгоритмов их выбора, результатов применения, а также отладчик и исходный код.
В литературе есть такое описание общего принципа.
Допустим, у вас есть такое логическое дерево и соответственно memo:
Далее, правила преобразования могут сгенерировать:
— логический оператор эквивалентный той же группе, например, join(a,b)=join(b,a)
— физический оператор, например, join -> merge join.
— либо набор логических операторов, которые формируют связанный под-план; при этом его вершина записывается в исходную группу, а другие операторы, могут распределиться по разным группам, в том числе, породить новые. Например, join (A,join(B,C))=join((A,B),C).
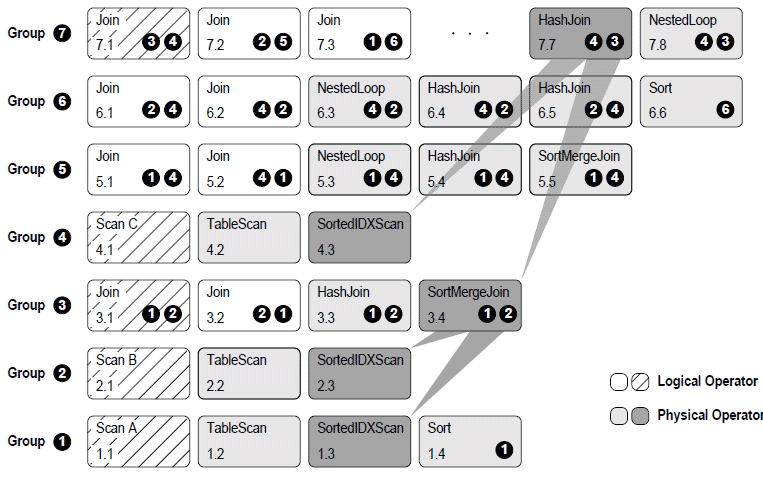
Таким образом, первоначальная структура memo может преобразиться как:
Серым – отмечены физические операторы.
Темно-серым – выбранные для плана.
Однако, как только, я пробовал применить теорию на практике, сразу стало понятно, что некоторые ключевые детали в описании алгоритмов отсутствуют. Давайте, на нашем примере, попробуем нарисовать похожую картинку и выбрать осмысленный план.
Особо, я подчеркну тот факт, что оптимизатор не то, что имеет «немного другой» алгоритм, он имеет совсем другой, более сложный и совершенный механизм генерации альтернатив и поиска плана, о котором, наверное, можно написать отдельную книгу. Кое-какое его описание удалось выискать по крупицам в публичной литературе, и оно будет приведено позже. А пока, давайте попробуем, найти способ использовать исходную структуру Memo самостоятельно, чтобы выбрать план. Забегая вперед, есть ли возможность посмотреть на финальный вид memo, который будет использован для построения плана – да есть. По этому, действия ниже, можно назвать в некотором роде «подгонкой под ответ», и хотя каждое действие я старался обосновать логически, я не могу утверждать, что оптимизатор действует именно с такой логикой.
Для сохранения логических связей мы будем обозначать группы, которые породили новую группу, и группы которые являются прямыми потомками группы. Кроме того, давайте типы операций — логических, скалярных и физических, обозначим просто цветом, чтобы не загромождать схемы:
— зеленым логические операторы;
— серым скалярные;
— красным физические операторы.
Вот как выгладит наше первоначальное дерево:
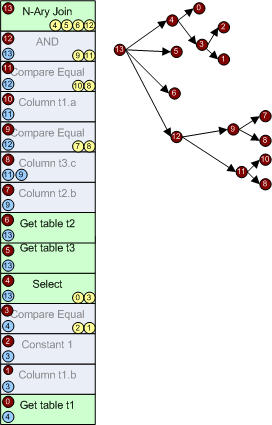
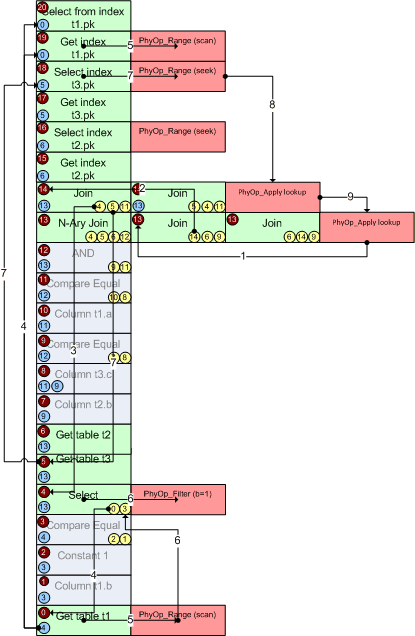
Теперь, выстроим, все операторы в один столбец и пропишем родителей (обозначено синим) и потомков (обозначено желтым), а также я приведу изначальное логическое дерево в сокращенном виде.
Это, то же самое, что и предыдущий рисунок, только записано по-другому.
Теперь, при помощи правил преобразования (механизм, о котором мы говорили в части посвященной тривиальному плану), начнем генерировать эквиваленты.
Сначала раскроем Nary Join Operator. Оператор N-арного соединения. Интуитивно понятно, что если бинарное соединение принимает на вход две таблицы, N-арное, N – таблиц, но что это такое применительно к процессу оптимизации? К сожалению, никакой информации по SQL Server по этому поводу я нигде не нашел. Однако, в документации к Sybase, встречается описание этого оператора применительно к процессу оптимизации. В частности там сказано, что оператор NARY JOIN используется только в процессе оптимизации и никогда не оценивается непосредственно, он используется, когда оптимизатор встречает серию из двух и более join-ов (довольно похоже на нашу картину). Учитывая, что изначально это были родственные продукты, то возможно какой-то похожий смысл в него вложен и тут, будем считать, что это просто логическое операция соединения, если соединяемых операндов более трех.
Заметьте, что еще на этапе дерева логических операций, таблицы у нас перечисляются не в исходном порядке: t1 join t2 join t3, а в измененном t1 join t3 join t2. Это было сделано благодаря этапу эвристической оценки порядка соединений, на этапе упрощения.
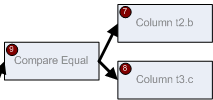
Итак, разобьем соединение t1 join t3 join t2, следующим образом: (t1 join t3) join t2. Т.е. сначала выполним соединение t1 и t3, а потом выполним соединение этого результата с t2.
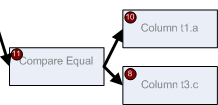
Соединение t1 и t3 у нас, согласно нашему логическому дереву, может быть выполнено по колонкам t1.a и t3.c помощью скалярного оператора сравнения этих колонок:
Таким образом, в группе, которая представляет это соединение, участвуют дочерние группы 4,5,11. Также, поскольку в нашем дереве нет эквивалентного логического оператора соединения двух этих таблиц, этот оператор образует новую группу 14. Запишем ее в верх memo.
Теперь, соединение этой новой группы с таблицей t2. Оно может быть выполнено по колонкам t3.c и t2.b.
Поскольку это соединение группы 14 и t2 эквивалентно общему логическому выражению соединению трех таблиц, данное соединение не образует новой логической группы, а записывается в эквиваленты группе 13.
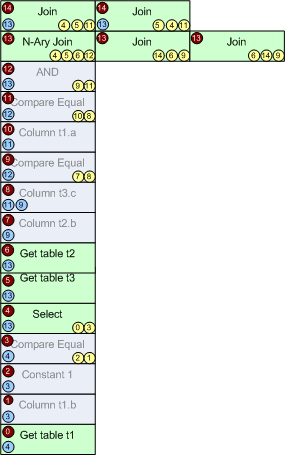
В итоге, вот как выглядит memo и дерево логических операторов.
Теперь, давайте применим правило коммутативного соединения (JoinCommute), которое можно выразить как (A join B)=(B join A). Применим его к операторам внутри групп 13 и 14, поскольку получающиеся в результате правила преобразования операторы будут логическими эквивалентами, то для них не создаются новые группы, и они помещаются в группы эквиваленты 13 и 14 соответственно (запишем справа от соответствующих групп).
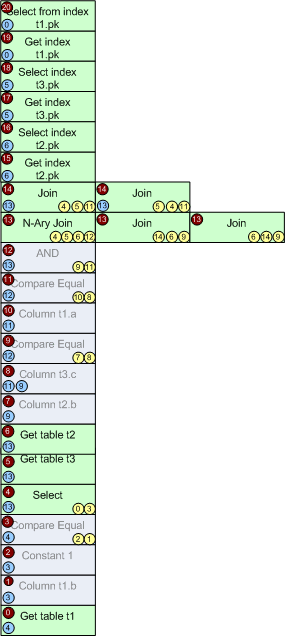
Теперь, поговорим о стратегии доступа к таблицам. Это может быть просмотр кластерного индекса (обозначим операцию как Get index) или поиск по кластерному индексу (обозначим операцию как Select from Index). Для операторов Get table из групп 6,5,1 – применим соответствующие правила, и полученные операторы просмотра индекса и поиска по индексу запишем в новые группы (т.к. эквивалентных им логических операторов у нас в memo пока нет).
Это будут группы 15,16 для таблицы t2; 17,18 для таблицы t3; 19,20 для t1.
Вот как выглядит структура memo после этого.
Теперь, будем применять implementation rules, т.е. правила генерации физических операций.
Но прежде, сделаем небольшое лирическое отступление, на тему физического выполнения Nested Loops Join.
Выполните запросы, и сравните планы:
select * from t1 join t2 on t1.a = t2.b join t3 on t2.b = t3.c where t1.b = 1 option(recompile ,querytraceon 3604 ,querytraceon 8606 ) select * from t1 cross apply (select * from t2 where t1.a = t2.b) t2 cross apply (select * from t3 where t2.b = t3.c) t3 where t1.b = 1 option(recompile ,querytraceon 3604 ,querytraceon 8606 )
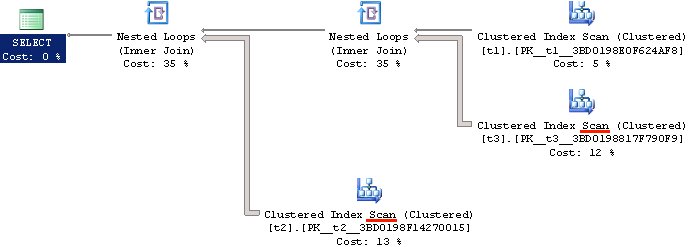
Планы окажутся абсолютно идентичными по структуре и стоимости:
Если мы посмотрим на входное дерево логических операций и упрощенное, в случае второго запроса, то мы увидим, что логический оператор Apply был заменен на Join:
*** Input Tree: ***
LogOp_Project QCOL: [opt].[dbo].[t1].a QCOL: [opt].[dbo].[t1].b QCOL: [opt].[dbo].[t1].c QCOL: [opt].[dbo].[t2].b QCOL: [opt].[dbo].[t2].c QCOL: [opt].[dbo].[t2].d QCOL: [opt].[dbo].[t3].c
LogOp_Select
LogOp_Apply (x_jtInner)
LogOp_Apply (x_jtInner)
…
*** Simplified Tree: ***
LogOp_Join
LogOp_Join
LogOp_Select
LogOp_Get TBL: t1 t1 TableID=226099846 TableReferenceID=0 IsRow: COL: IsBaseRow1001
…
Однако, на уровне физических операторов, оба запроса были выполнены при помощи физического оператора PhyOp_Apply lookup.
В данном случае, за это отвечает правило AppIdxToApp.
Попробуйте отключить его и выполнить оба запроса (с подсказкой loop join, чтобы сервер не поменял тип соединения).
dbcc ruleoff('AppIdxToApp')
select *
from
t1
join t2 on t1.a = t2.b
join t3 on t2.b = t3.c
where
t1.b = 1
option(recompile
,loop join
)
select *
from
t1
cross apply (select * from t2 where t1.a = t2.b) t2
cross apply (select * from t3 where t2.b = t3.c) t3
where
t1.b = 1
option(recompile
,loop join
)
dbcc ruleon('AppIdxToApp')
Вы увидите, что план поменялся:
Теперь оба запроса выполняют сканирование кластерного индекса, и в данном случае, Nested Loops, действительно выполняется при помощи физического оператора PhyOp_LoopsJoin. Убедиться в этом, вы позже сможете самостоятельно, когда мы дойдем до просмотра выходного дерева физических операций.
Зная про этот механизм, а также заранее зная, что в нашем случае план построится с поиском по кластерному индексу таблиц t2,t3, а не просмотром, то в качестве физического оператора соединения, в memo мы будем применять оператор PhyOp_Apply lookup, а не PhyOp_LoopsJoin.
Посмотрим структуру с физическими операторами (пояснения даны ниже).
Начнем с корневой группы и самого первого логического эквивалента N-арного соединения – join 14,6,9.
1. Попробуем применить правило и сгенерировать физический оператор PhyOp_Apply lookup. Однако, в таком случае, соединяемые группы тоже должны содержать физические операторы.
Посмотрим на соединяемые группы: 14 и 6.
2. Первая группа – 14, это тоже соединение, в ней самый первый начальный эквивалент – это соединение групп 4,5,11.
3.Смотрим на группу 4 (Select), это результат выборки из группы 0 (Get table t1) и применения фильтра из группы 3 (Compare equal), сравнения колонки b с константой 1.
4. Посмотрим на группу 0 и те группы, которые от нее были порождены (мы обозначали родительские группы цифрой в синем кружке слева). Это группы 19(Get index t1.pk) и 20(Select from index t1.pk),. Поскольку, у нас нет никаких индексов, нам придется просканировать всю таблицу или весь кластерный индекс, а после отфильтровать данные по колонке b. В этом случае, Cardinality, будет равно 1000 строк, значит, выгоднее будет применить сканирование, по этому, генерируем физические альтернативы, только для групп 0, 19.
5. Получение данных из таблицы (причем, как поиск, так и просмотр) осуществляется оператором PhyOp_Range, в скобках уточним, что это именно просмотр. В нашем случае, индекс кластерный, по этому, что просмотр таблицы, что просмотр индекса – операции эквивалентные, по этому, будем использовать результат, например первого эквивалента из группы 0.
6.Сравнение колонки со значением при помощи скалярного оператора. Фильтрация по значению, осуществляется оператором PhyOp_Filter.
7. Теперь, группа вторая соединяемая группа – 5 (Get table t3). Посмотрим, какие группы были порождены от группы 5. Это группы 17 (Get index t3.pk) и 18 (Select from index t3.pk). Произведя анализ, оптимизатор решает, что в данном случае, будет выгодно использовать поиск по индексу, а не просмотр, поэтому выбирает группу 18. Однако, в ней логический оператор, поэтому сгенерируем в этой же группе эквивалентный физический оператор PhyOp_Range (seek).
8. Теперь, в группе 14, все соединяемые группы содержат физические операторы, и для оператора join мы можем сгенерировать физический эквивалент PhyOp_Apply lookup.
9. Теперь, вернемся к первому соединению. С группой 14 разобрались, теперь, группа 6.
По аналогии с группой 5, посмотрим, какие группы были порождены от 6 — это 19,20. Выбираем ту, что с поиском по индексу и генерируем в ней физический эквивалент PhyOp_Range (seek).
В итоге, все группы в соединении теперь имеют физические операторы, а значит для этой группы, мы тоже можем сгенерировать физический эквивалент PhyOp_Apply lookup.
Что дальше? После того, как может быть получено дерево, состоящее полностью из физических операторов, получено, вычисляется стоимость каждого оператора и его альтернатив. После этого, значение сравнивается, с внутренним порогом оптимизатора и если стоимость найденного плана проходит этот порог, то план считается достаточно хорошим и оптимизация прекращается.
Этот алгоритм обхода и анализа memo довольно примитивный, однако он позволяет проиллюстрировать принцип. В реальности оптимизатор использует более сложные алгоритмы, а также выполняет ряд других действий по анализу и поиску вариантов.
В частности это:
— анализ сложных случаев, например, когда логический оператор join не требует сортировки, а его физическая реализация merge join требует, тогда, может ли быть выбран merge join, зависит от требований других операторов – все эти случаи учитываются;
— поиск и распознавание дубликатов, саамы простой случай, бесконечная перестановка JoinCommute, A join B -> B join A -> A join B и т.д. У оптимизатора, есть механизмы борьбы с замкнутыми цепочками и удаления лишних групп;
— для каждого оператора, поддерживаются сведения о его стоимости и стоимости его дочерних физических операторов, т.е. поддерева;
— по каждой группе, ведется отслеживание минимального по стоимости физического оператора эквивалента и его поддерева, и при оценке нового оператора, в его стоимость входит наилучшая стоимость его дочерних операторов;
— в оптимизаторе существует некий планировщик примитивов, в котором реализованы разные стратегии, благодаря которым решается, применять правило преобразование или нет;
— ограничительные эвристические алгоритмы на основе анализа стоимостей позволяют избегать раскрытия потенциально дорогостоящих альтернатив, которые с учетом текущего состояния оптимизации не могут быть подпланами оптимального плана;
Это только то, что я смог найти. Наверняка есть и еще какие-то механизмы. Поэтому, когда мы посмотрим на реальную конечную структуру memo, она будет отличаться, в данном случае совсем чуть-чуть, т.к. запрос очень простой и вариантов у оптимизатора было не много. В случае же реального запроса, я бы не взялся предсказывать результат. Если вы, например, всего лишь, вернете индекс ix_b, в таблице t1, по столбцу b – то количество групп уже возрастет до 33. Если представить себе реальный запрос, с кучей таблиц, индексов, подзапросов и вариантов, то легко понять, почему количество групп может измеряться тысячами.
Но прежде чем мы посмотрим, на реальную структуру memo для этого запроса, мне бы хотелось затронуть еще одну тему, тему оценок. Как мы уже говорили выше, когда оптимизатор строит план, он оценивает операторы.
Оценки
Оценки могут зависеть от многих факторов, например, от количества строк, типа оператора, свойств оператора и т.д. А оценка узлов подплана оператора, складывается из оценки самого оператора + сумма оценок всего его дочерних узлов.
При оценке оператора большую роль играет число строк, многие знают, что оптимизатор способен определить число строк с использованием статистики.
Например, рассмотрим запрос:
select * from t1 where b = 1 option (recompile)
прим. Опция recompile нужна тут и в нижеследующих запросах, чтобы исключить влияние переиспользования планов при простой параметризации, если вы планируете выполнять запросы несколько раз с разными значениями.
Количество строк оценено как 10:
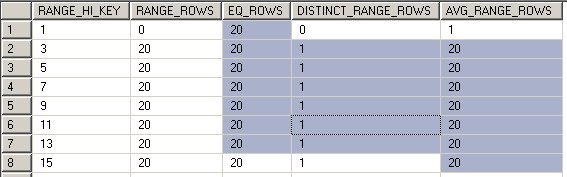
И действительно, если мы выполним запрос для просмотра статистики по колонке b
declare @sql nvarchar(max);
select
@sql = 'dbcc show_statistics(t1,' + name + ') with histogram'
from
sys.stats s
join sys.stats_columns sc on s.[object_id] = sc.[object_id] and s.stats_id = sc.stats_id
where
s.[object_id] = object_id('t1') and sc.column_id = columnproperty(s.[object_id],'b','ColumnId')
exec (@sql)
В диапазоне до единицы, для верхнего значения границы «1», значение EQ_ROWS = 10. Если бы мы взяли значение, не совпадающее со значением верхней границы диапазона статистики, например, «2», то мы бы смотрели на колонку AVG_RANGE_ROWS, следующего ряда, т.к. 2 попадает в диапазон — (1;3], которое в прочем тоже составляет 10, в данном случае.
Итак, 10 строк, селективность для данного предиката равняется количество для данного значения согласно статистике, разделенное на общее число строк.
Селективность запроса: 10/1000 = 0.01.
Для предиката, в котором участвует неравенство, значения суммируются, например:
select * from t1 where c < 15 option (recompile)
Будут просуммированы значения EQ_ROWS + AVG_RANGE_ROWS:
Результат 280.
Селективность: 280/1000 = 0.28.
Как оценить количество строк в запросе, когда в нем участвуют сразу два предиката, соединенные по условию and?
select * from t1 where b = 1 and c < 15 option (recompile)
По сути, нам надо оценить мощность пересечения множеств, и логичным будет перемножить селективности двух этих запросов и умножить на общее число строк:
0.01*0.28 = 0.0028.
1000* 0.0028= 2.8 строк.
Проверим:
Теперь, как оценить количество строк в запросе, когда в нем условие or? В таком случае, нам надо сложить количества строк, возвращаемые по первому условию, количество строк по второму условию, и убрать пересечение этих множеств, а пересечение мы нашли в предыдущем разделе, это 2,8 строки.
Итого: (10+280)-2.8 = 287.2 строк.
Проверяем:
select * from t1 where b = 1 or c < 15 option (recompile)
Теперь, вернемся к нашему запросу, и перейдем от оценок количества строк непосредственно к вычислению стоимости плана.
В оценке стоимости используются некие «магические числа», на самом деле, они не магические, а были когда-то измерены на конкретном оборудовании, но теперь имеют условный характер.
Например, в текущей модели оценки, одна операция случайного доступа оценивается как 1/320 (т.е. 320 страниц в единицу времени), а последовательного 1/1350 ( т.е. при последовательном доступе за единицу времени можно прочитать 1350 страниц), что дает нам числа: 0.003125 случайный IO и 0.00074074 последовательный. Процессорная стоимость зависит от оператора.
Давайте посчитаем стоимость Clustered Index Scan t1.
Стоимость CPU: 0.0001581 + 0.0000011*(n-1), где n — кол-во строк в индексе.
Стоимость IO: 0.003125 (одна случайная операция доступа) + 0.00074074*(p-1), где p — кол-во страниц занимаемых индексом (остальные страницы последовательный доступ).
Стоимость оператора: Operator Cost = CPU+IO
Стоимость поддерева: Subtree Cost = Operator Cost + Subtree Cost(child). Т.к. это у нас самый листовой уровень, то у него нет поддеревьев, так что, их стоимость равна 0.
Посчитаем:
CPU: 0.0001581 + 0.0000011*999 = 0.0012570.
IO: 0.003125 + 0.00074074*(3-1) = 0.00460648, где 3 количество страниц в индексе, можно получить так:
select page_count from sys.dm_db_index_physical_stats(db_id(),object_id('t1'),null,null,null) where index_id = 1
Operator Cost: 0.0012570+0.00460648 = 0.00586348
Subtree Cost: 0.00586348
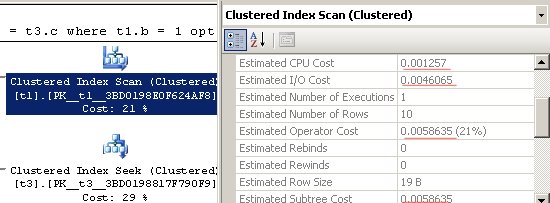
Посмотрим в план:
Стоимости совпали, кроме того, что SSMS округлил 0.00460648 до 0.0046065. Если посмотреть в представление плана как xml, то там округления нет:
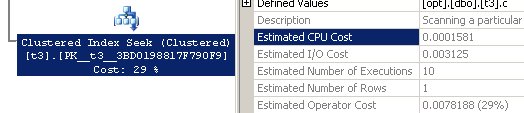
Для операторов Clustered Index Seek (lookup) по t2 и t3, в полях Estimated CPU Cost, Estimated IO Cost, отображаются значения только для одной операции, однако в поле Estimated Operator Cost, находятся данные уже с учетом 10 выполнений.
При этом, если просто просуммировать стоимость CPU и IO для каждого выполнения, то вы не получите исходную цифру в данном случае.
Путем многочисленных экспериментов на разных таблицах, я пришел к выводу, что процессорная составляющая действительно равна EstimatedNumberOfExecutions*0.0001581. Однако, IO вычисляется по более сложной формуле, условно, на данный момент, я бы представил ее как:
IO = 0.003125 + 0.003125*(n-1)*Q(p);
Где, n – число выполнений, Q – некая функция (которая, насколько я смог выяснить, содержит некую экспоненциальную составляющую), а p – количество страниц, причем не того индекса по которому делается lookup, а того, для которого делается этот поиск.
Более подробной или достоверной информации, к сожалению, на эту тему раздобыть пока не удалось, по этому, пока, просто примем эти оценки как есть.
Теперь, оценка Nested Loop Join.
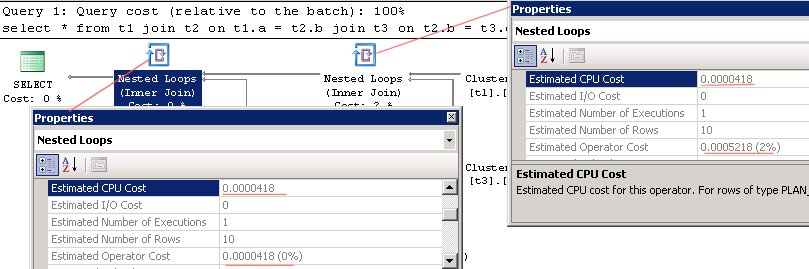
Для данного случая, оценка довольно простая. Стоимости IO данный оператор не имеет, а CPU вычисляется как n*0.00000418, где n – количество строк, в данном случае 10.
Итого, стоимость операторов 0.0000418, и состоит лишь из стоимости CPU.
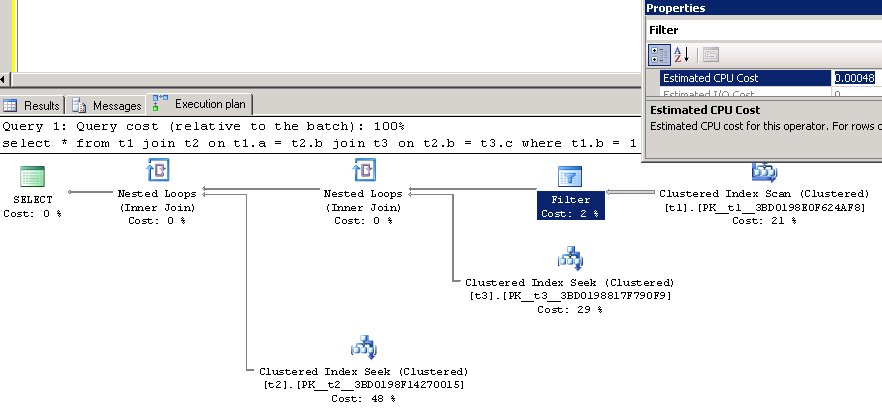
Однако, заметьте, это справедливо в случае только самого левого join, во втором, стоимость возросла, хотя при этом, стоимость процессорной составляющей не изменилась, и стоимости IO тоже не появилось. Откуда же эта «добавочная стоимость»? Вспомним про операцию Filter. Ее стоимость в плане включена в Nested Loops Join и составляет: 0.00048. Вы позже увидите это в memo, если вы сложите 0.0000418 и 0.00048, вы получите 0.0005218.
Есть способ выполнить запрос так, чтобы план не включал операцию Filter в стоимость Nested Loops,а выделил ее в отдельный оператор.
При этом, операция фильтрации не должна настораживать в смысле производительности, ведь заметьте, она производится до соединения, а значит в соединении уже участвуют только нужные строки, которых всего 10. Тот самый predicate pushdown. Применение этой операции абсолютно оправдано, т.к. мы сканируем индекс целиком, и нужно же как-то отфильтровать только необходимые строки.
Итак, у нас есть все стоимости,
Если мы сложим их:
Clustered Index Scan t1- 0.00586348
Filter — 0.00048
Clustered Index Seek t3 — 0.0078188
Nested Loops Join — 0.0000418
Clustered Index Seek t2 — 0.0131424
Nested Loops Join — 0.0000418
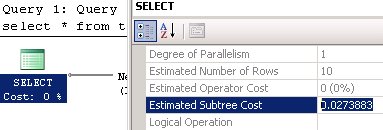
То мы получим общую оценку:
0.02738828
Если округлить до 7 знаков после запятой, 0.0273883, то мы увидим, что она полностью совпадает с:
Итак, с оценками разобрались. Но прежде чем вернуться к memo, позвольте дать комментарий по еще трем понятиям: Rebinds, Rewinds, Row Goal — т.к. эти значения присутствуют в выводе информации о memo.
Rebinds и Rewinds – описаны в BOL. Коротко говоря, Rebinds – это число сбросов на начало, а Rewinds, число повторного использования внутреннего цикла (сейчас, я говорю об этих конструкциях только в рамках вложенных циклов).
Что это значит на практике.
Представьте, что во внешнем цикле, мы перебираем последовательно значения, получили первое значение, допустим — 1. Теперь, во внутренним, мы ищем все строки в соединяемой таблице со значением 1 в соединяемой колонке. Находим первую, включаем в результат, что дальше?
Дальше, если мы ничего не знаем о столбце таблицы во внутреннем цикле, мы обязаны продолжить поиск, т.е. не меняя значения во внешнем цикле, продолжить поиск во внутреннем – это будет rewind. Если же, мы знаем, что найденная строка во внутренней таблице со значением 1 в соединяемом столбце – единственная, то мы можем прекратить поиск по внутренней таблице, вернуться во внешнюю, изменить искомое значение, сбросить внутренний цикл на начало и повторить поиск – это будет rebind.
Рассмотрим пример:
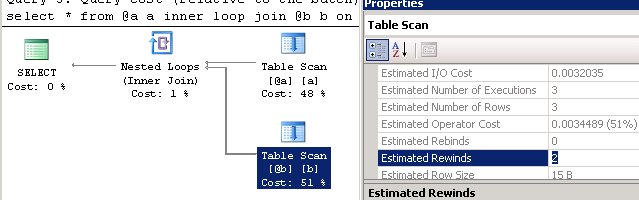
declare @a table(a int, c int); declare @b table(b int, c int); insert @a values (1,1),(2,2),(3,3); insert @b values (1,1),(2,2),(3,3); select * from @a a inner loop join @b b on a.a = b.b option(recompile)
Т.к. нам ничего не известно о столбце @b.b, то после первой итерации, мы повторяем поиск по внутренней таблице с неизменившимся условием поиска по значению 1 — получаем rewind.
Теперь, давайте дадим оптимизатору информацию о том, что если мы во внутренней таблице уже нашли совпадающее значение, то оно единственное и можно передвинуть счетчик во внешнем цикле, по внешней таблице и выполнять поиск уже для нового значения. Для этого, создадим первичный ключ по @b.b.
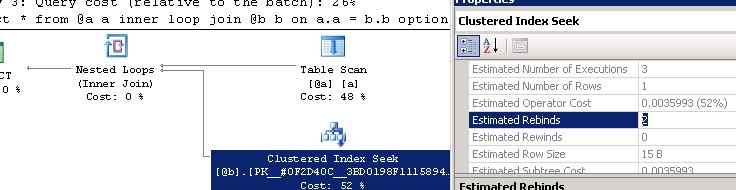
declare @a table(a int, c int); declare @b table(b int primary key, c int); insert @a values (1,1),(2,2),(3,3); insert @b values (1,1),(2,2),(3,3); select * from @a a inner loop join @b b on a.a = b.b option(recompile)
Теперь, мы видим, что в оценке используются rebinds. Т.е. сразу, как только во внутренней таблице было найдено значение – происходит прерывание внутреннего цикла и смена искомого значения во внешнем.
Прим. Зачем здесь option(recompile)? Помните, что мы говорим об оценках. А для табличных переменных статистика не собирается, и единственным способом оценить число строк (и соответственно число выполнений, а, следовательно, число rebinds/rewinds, является рекомпиляция на момент, когда таблицы уже заполнены.
Теперь, немного коснемся концепции RowGoal.
RowGoal – или, дословно, «цель строк», это механизм, используемый сервером в том случае, если заранее известно число строк, которые необходимо получить. Это могут быть конструкции – TOP, FAST n, EXISTS и т.д. В этом случае, оптимизатор, заранее зная какой нужно получить результат, может ограничивать более ранние в плане операторы, по количеству строк.
Его особенность и отличие от оценки Cardinality в том, что если оценка Cardinality идет по плану снизу вверх, то оценка RowGoal, идет сверху вниз.
Рассмотрим пример:
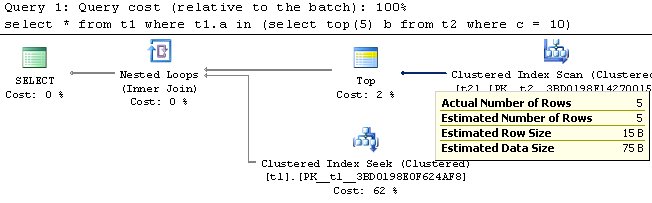
select * from t1 where t1.a in (select top(5) b from t2 where c = 10)
План запроса:
В данном случае, как можно видеть, уже на этапе просмотра кластерного индекса значение ограничено 5 строками. Обратите внимание, что оценка производится до предложения top!
Т.е. еще до того как будет применен оператор ограничения, мы уже выбираем из кластерного индекса всего 5 строк. Это достигается за счет механизма RowGoal. Более подробно расписывать этот механизм – это отдельная статья, к тому же, она уже написана, рекомендую ознакомиться тут (eng).
Теперь, вернемся к нашему memo, и наконец, посмотрим на его реальную структуру.
Для начала, вспомним то, то что мы получили:
А теперь, выполним запрос с очередным недокументированным флагом трассировки 8615.
select * from t1 join t2 on t1.a = t2.b join t3 on t2.b = t3.c where t1.b = 1 option(recompile ,querytraceon 3604 ,querytraceon 8615 )
Результат:
--- Final Memo Structure --- Group 21: Card=1 (Max=1, Min=0) 0 LogOp_SelectRes 20 3 Group 20: Card=1 (Max=1, Min=0) 0 LogOp_SelectIdx 19 11 Group 19: Card=1000 (Max=10000, Min=0) 1 PhyOp_Range 1 ASC Cost(RowGoal 0,ReW 0,ReB 0,Dist 0,Total 0)= 0.00586348 0 LogOp_GetIdx Group 18: Card=1 (Max=1, Min=0) 1 PhyOp_Range 1 ASC 11.0 Cost(RowGoal 0,ReW 0,ReB 9,Dist 10,Total 10)= 0.00781879 0 LogOp_SelectIdx 17 11 Group 17: Card=1000 (Max=10000, Min=0) 0 LogOp_GetIdx Group 16: Card=1 (Max=1, Min=0) 1 PhyOp_Range 1 ASC 9.0 Cost(RowGoal 0,ReW 0,ReB 9,Dist 10,Total 10)= 0.0131424 0 LogOp_SelectIdx 15 9 Group 15: Card=1000 (Max=10000, Min=0) 0 LogOp_GetIdx Group 14: Card=10 (Max=10000, Min=0) 2 PhyOp_Applyx_jtInner 4.2 18.1 Cost(RowGoal 0,ReW 0,ReB 0,Dist 0,Total 0)= 0.0142041 1 LogOp_Join 5 4 11 0 LogOp_Join 4 5 11 Root Group 13: Card=10 (Max=10000, Min=0) 3 PhyOp_Applyx_jtInner 14.2 16.1 Cost(RowGoal 0,ReW 0,ReB 0,Dist 0,Total 0)= 0.0273883 2 LogOp_Join 6 14 9 1 LogOp_Join 14 6 9 0 LogOp_NAryJoin 4 5 6 12 Group 12: 0 ScaOp_Logical 9 11 Group 11: 0 ScaOp_Comp 10.0 8.0 Cost(RowGoal 0,ReW 0,ReB 0,Dist 0,Total 0)= 3 Group 10: 0 ScaOp_Identifier Cost(RowGoal 0,ReW 0,ReB 0,Dist 0,Total 0)= 1 Group 9: 0 ScaOp_Comp 7.0 8.0 Cost(RowGoal 0,ReW 0,ReB 0,Dist 0,Total 0)= 3 Group 8: 0 ScaOp_Identifier Cost(RowGoal 0,ReW 0,ReB 0,Dist 0,Total 0)= 1 Group 7: 0 ScaOp_Identifier Cost(RowGoal 0,ReW 0,ReB 0,Dist 0,Total 0)= 1 Group 6: Card=1000 (Max=10000, Min=0) 0 LogOp_Get Group 5: Card=1000 (Max=10000, Min=0) 0 LogOp_Get Group 4: Card=10 (Max=10000, Min=0) 2 PhyOp_Filter 0.2 3.0 Cost(RowGoal 0,ReW 0,ReB 0,Dist 0,Total 0)= 0.00634348 0 LogOp_Select 0 3 Group 3: 0 ScaOp_Comp 1.0 2.0 Cost(RowGoal 0,ReW 0,ReB 0,Dist 0,Total 0)= 3 Group 2: 0 ScaOp_Const Cost(RowGoal 0,ReW 0,ReB 0,Dist 0,Total 0)= 1 Group 1: 0 ScaOp_Identifier Cost(RowGoal 0,ReW 0,ReB 0,Dist 0,Total 0)= 1 Group 0: Card=1000 (Max=10000, Min=0) 2 PhyOp_Range 1 ASC Cost(RowGoal 0,ReW 0,ReB 0,Dist 0,Total 0)= 0.00586348 0 LogOp_Get ----------------------------
Теперь, если представить это в табличной структуре, то мы увидим:
Какие мы видим различия.
Во-первых, есть дополнительная группа 21, по счету 22-ая, в которой есть дополнительный логический оператор. Во-вторых, фильтр и сканирование таблицы записались в эквиваленты 2.
Эти различия понятны, т.к. я еще раз подчеркиваю, что реальный алгоритм построения memo отличен от того что мы проходили по шагам. Он гораздо сложнее.
Например, если бы мы не удалили индекс ix_b, то оптимизатору потребовалось бы 33 группы для анализа возможных вариантов, если бы таблицы имели разную Cardinality, то потребовалось бы больше шагов, чтобы исследовать больше вариантов соединений и т.д. Также стали бы появляться новые логические и физические операторы, а к ним применятся новые правила преобразования. В итоге, чем сложнее запрос, тем больше вариантов приходится исследовать оптимизатору и тем больше структура memo.
Может ли процесс поиска альтернатив продолжаться до бесконечности, если не найден достаточно хороший план? Конечно, нет, для ограничения времени поиска плана до разумного, используется концепция таймаутов. Таймаут задается не временем, а неким значением, представляющего собой что-то вроде бюджета на количество задач оптимизации, который выделяет себе оптимизатор в зависимости от сложности запроса. Как только этот бюджет полностью выбран, а план все еще не достаточно дешев – оптимизатор должен либо перейти на следующую стадию, либо вернуть план.
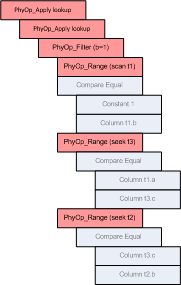
И, наконец, после того, как структура memo заполнена, оценки альтернатив проведены и выбраны операторы с наименьшей стоимостью, строится дерево физических операторов. Если мы, последовательно пройдемся по стрелкам в нашем memo, выбирая физические операторы, то мы получим:
В очередной раз, сравним с выводом оптимизатора. Запустим наш запрос, с недокументирвоанным флагом трассировки 8607, которые покажет выходное дерево физических операций.
select * from t1 join t2 on t1.a = t2.b join t3 on t2.b = t3.c where t1.b = 1 option(recompile ,querytraceon 3604 ,querytraceon 8607 )
Результат:
*** Output Tree: ***
PhyOp_Apply lookup TBL: t2 (0) (x_jtInner)
PhyOp_Apply lookup TBL: t3 (0) (x_jtInner)
PhyOp_Filter
PhyOp_Range TBL: t1(1) ASC Bmk ( QCOL: [opt].[dbo].[t1].a) IsRow: COL: IsBaseRow1001
ScaOp_Comp x_cmpEq
ScaOp_Identifier QCOL: [opt].[dbo].[t1].b
ScaOp_Const TI(int,ML=4) XVAR(int,Not Owned,Value=1)
PhyOp_Range TBL: t3(1) ASC Bmk ( QCOL: [opt].[dbo].[t3].c) IsRow: COL: IsBaseRow1007
ScaOp_Comp x_cmpEq
ScaOp_Identifier QCOL: [opt].[dbo].[t1].a
ScaOp_Identifier QCOL: [opt].[dbo].[t3].c
PhyOp_Range TBL: t2(1) ASC Bmk ( QCOL: [opt].[dbo].[t2].b) IsRow: COL: IsBaseRow1004
ScaOp_Comp x_cmpEq
ScaOp_Identifier QCOL: [opt].[dbo].[t2].b
ScaOp_Identifier QCOL: [opt].[dbo].[t3].c
********************
** Query marked as Cachable
********************
Как вы видите, используется физический оператор PhyOp_Apply lookup. Теперь, вы можете вернуться чуть назад, отключить правило и выполнить запрос с этим флагом трассировки, чтобы убедиться, что тогда будет использоваться PhyOp_LoopsJoin.
Ну и напоследок, выполним запрос, который удовлетворяет условиям тривиального плана, со включенными флагами, дерева логических операторов, начального и конечного memo, и выходным деревом физических операторов.
select * from t1 option(recompile ,querytraceon 3604 --вывод на консоль ,querytraceon 8606 --дерево логических операторов ,querytraceon 8608 --начальное мемо ,querytraceon 8615 --конечное мемо ,querytraceon 8607 --дерево физических операторов )
Результат (начальный вывод частично сокращен):
…
*****************************************
*** Tree After Project Normalization ***
LogOp_Get TBL: t1 t1 TableID=226099846 TableReferenceID=0 IsRow: COL: IsBaseRow1001
****************************************
*** Output Tree: (trivial plan) ***
PhyOp_NOP
PhyOp_Range TBL: t1(1) ASC Bmk ( QCOL: [opt].[dbo].[t1].a) IsRow: COL: IsBaseRow1001
********************
Как мы убеждаемся, для тривиального плана memo не строится, что значит, выбора на основе стоимости не осуществляется.
На этом закончим разговор о стадии search 0 и перейдем к стадии search 1, в которой мы поговорим о поиске параллельного плана. Надеюсь, было интересно.
upd. 12.05.2012
Недавно нашел еще один флаг 8612, он позволяет включить в деревья (которые выводятся при помощи флагов 8605, 8606, 8607) информацию из memo, например о кардинальности или о стоимости, если мы говорим о выходном дереве операторов.
Например, вот так выглядит более подробное выходное дерево, для запроса из примера:
*** Output Tree: ***
PhyOp_Apply lookup TBL: t2 (0) (x_jtInner) [ Card=10 Cost(RowGoal 0,ReW 0,ReB 0,Dist 0,Total 0)= 0.0273883 ]
PhyOp_Apply lookup TBL: t3 (0) (x_jtInner) [ Card=10 Cost(RowGoal 0,ReW 0,ReB 0,Dist 0,Total 0)= 0.0142041 ]
PhyOp_Filter [ Card=10 Cost(RowGoal 0,ReW 0,ReB 0,Dist 0,Total 0)= 0.00634348 ]
PhyOp_Range TBL: t1(1) ASC Bmk ( QCOL: [opt].[dbo].[t1].a) IsRow: COL: IsBaseRow1001 [ Card=1000 Cost(RowGoal 0,ReW 0,ReB 0,Dist 0,Total 0)= 0.00586348 ]
ScaOp_Comp x_cmpEq
ScaOp_Identifier QCOL: [opt].[dbo].[t1].b
ScaOp_Const TI(int,ML=4) XVAR(int,Not Owned,Value=1)
PhyOp_Range TBL: t3(1) ASC Bmk ( QCOL: [opt].[dbo].[t3].c) IsRow: COL: IsBaseRow1007 [ Card=1 Cost(RowGoal 0,ReW 0,ReB 9,Dist 10,Total 10)= 0.00781879 ]
ScaOp_Comp x_cmpEq
ScaOp_Identifier QCOL: [opt].[dbo].[t1].a
ScaOp_Identifier QCOL: [opt].[dbo].[t3].c
PhyOp_Range TBL: t2(1) ASC Bmk ( QCOL: [opt].[dbo].[t2].b) IsRow: COL: IsBaseRow1004 [ Card=1 Cost(RowGoal 0,ReW 0,ReB 9,Dist 10,Total 10)= 0.0131424 ]
ScaOp_Comp x_cmpEq
ScaOp_Identifier QCOL: [opt].[dbo].[t2].b
ScaOp_Identifier QCOL: [opt].[dbo].[t3].c
********************
** Query marked as Cachable





 PDF
PDF